
Introducción
En el ámbito de la ingeniería y la gestión de calidad, comprender la distribución normal (o de Gauss) y la desviación estándar es esencial para analizar procesos, establecer tolerancias y tomar decisiones basadas en datos. Este artículo explora estos conceptos clave con un enfoque técnico-divulgativo, ideal para profesionales que buscan aplicar estadísticas en entornos industriales.
¿Qué es la Distribución Normal?
La distribución normal es una función de probabilidad que describe cómo se distribuyen los datos alrededor de un valor central (la media). Es simétrica, con forma de campana, y aparece de forma natural en muchos procesos físicos, biológicos e industriales. Esto se debe al teorema del límite central, que establece que la suma de muchas variables independientes tiende a seguir una distribución normal, incluso si las variables originales no lo hacen.
La Desviación Estándar (σ)
La desviación estándar mide la dispersión de los datos respecto a la media. Cuanto mayor es σ, más dispersos están los datos; cuanto menor, más concentrados.
Visualización de diferentes valores de σ:
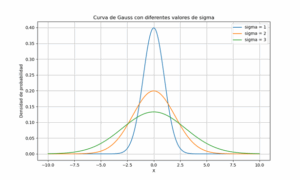
Como se observa, al aumentar σ, la curva se aplana y se ensancha, indicando mayor variabilidad en el proceso.
¿Por qué es importante en calidad?
En control de calidad, la desviación estándar permite evaluar la capacidad o el rendimiento de un proceso para mantenerse dentro de los límites de especificación. Esto se traduce en índices como por ejemplo el Pp, que compara la tolerancia total con la variabilidad del proceso, considerando la variación como 6 veces la desviación estándar:

Donde:
- USL: Límite superior de especificación
- LSL: Límite inferior de especificación
- σ: Desviación estándar del proceso
Impacto de los Límites de Tolerancia
Cuando se imponen límites de tolerancia, cualquier desviación significativa puede generar productos fuera de especificación. Visualmente:
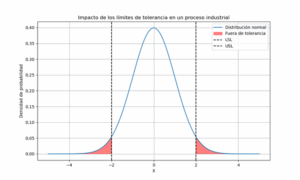
Las áreas rojas representan productos fuera de tolerancia, y representan el porcentaje de productos defectuosos sobre el total, habitualmente medidos en partes por millón (ppm). Un proceso bien centrado y con baja variabilidad minimizará estas áreas.
Conclusión
Comprender la distribución normal y la desviación estándar permite a ingenieros y responsables de calidad:
- Evaluar la estabilidad de procesos.
- Estimar el porcentaje de productos fuera de especificación.
- Tomar decisiones basadas en datos objetivos.
Estos conceptos son la base de herramientas como el Six Sigma, el SPC (Control Estadístico de Procesos) y la mejora continua.
